Loading... # 生成排列 ## next_permutation $next\_permutation$用于将一个范围内的排列转换为字典序大于它的最小排列(即下一个排列),用法如下: ```cpp while(next_permutation(beginIt, endIt)) { ...... } ``` 这样每次都会将$beginIt$和$endIt$范围内的数字变为下一个排列. 其单次运行最坏时间复杂度为$O(n)$, 在整个全排列序列上均摊下来是常数级的, 使用效果比较优秀. ## 原理 接下来研究一下它的原理。 对于一个特定的排列,例如`1 2 3 5 4`,可以考虑要生成下一个排列,应该如何变化。 显然变动应该发生在尽量靠右的位置。而如果某个部分是逆序,则不能变动,否则会变为已经出现过的排列,因为顺序总是先于逆序而出现的。 因此,我们要找到最靠近右侧的顺序对(最右端的正序的末尾),然后将它交换为逆序即可。 然而这个交换不能只是交换相邻的两个数,而应该整体考虑最右侧的逆序(递减序列)。例如`1 2 3 6 5 4`,如果仅仅交换3和6,就会得到`1 2 6 3 5 4`,显然不是我们要找的序列。我们已经确定了要变更的数字是3,那么就应该让它有**最小的变化**,也就是变为右侧逆序序列(一定延伸到序列尾,**但不一定都大于3**)的**比3大的最小元素**(这里是4),由于右侧序列单调减,所以顺序查找即可找到。(这里二分查找也可以,但不降低整体的时间复杂度,因为$O(n)$是第一步找顺序对的开销决定的。) 接下来,把4和3交换(此时右侧逆序序列仍然保持,因为其他数字既然大于4,也一定大于3),然后把右侧逆序序列reverse即可。 以下以一个综合一点的例子做演示: 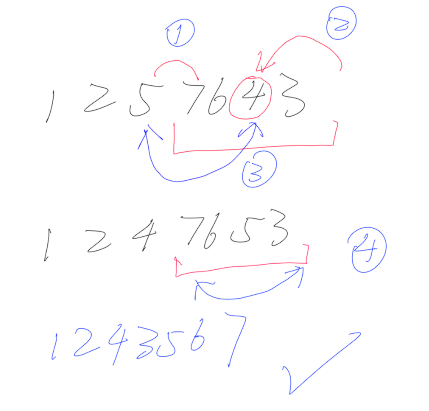 ## 代码实现 对[cppreference上给予的实现](https://zh.cppreference.com/w/cpp/algorithm/next_permutation)进行了少量更改并添加注释,增强了可读性,但这段代码已经不符合next_permutation应有的具名要求: ```cpp template <class BidirIt> bool next_permutation(BidirIt first, BidirIt last) { if (first == last) return false; BidirIt i = last; if (first == --i) return false; while (true) { BidirIt i1, i2; i1 = i; if (*--i < *i1) { // 如果i(即i1左侧)<i1,则找到了最右的顺序对 // 此时i1右侧是一个完整的逆序序列 i2 = last; while (*--i2 <= *i) ; std::iter_swap(i, i2);//i变为下一个元素即i2(i1到i2这个完整逆序里比他大的最小元素) std::reverse(i1, last);//原本的逆序里的元素变为顺序 return true; } if (i == first) { std::reverse(first, last); //当前已经是递减序列, 周而复始 return false; } } } ``` # 康托展开 对于全排列的朴素求解需要DFS以$O(n!)$的时间复杂度实现, 康托展开给予了一种$O(n^2)$时间复杂度的优异算法. ## 原理 巧妙地利用了计数方法. $$ 一个排列的序号 = 比它小的排列个数 + 1 $$ 接下来就可以按位依次枚举了, 我们用OI-wiki上的例子 $$ 2\quad5\quad3\quad4\quad1 $$ 第一位是$2$, 说明所有第一位为$1$的排列均先序于它, 共有$4!$个, 加入到我们的计数当中去. 第二位是$5$, 说明第二位为$1、2、3、4$的排列均大于他. 这里需要注意: 由于第一位已经确定为2, 所以这里只会有3个小于它的数字会出现在这里(可以**用树状数组维护有多少个小于他的数字前面还没出现过**), 每个都构成一个$3!$种的子排列, 所以第二位的贡献为$3*3!$. 以此类推, 第三位贡献为$1*2!$, 第四位贡献为$1*1!$, 第五位贡献为$0*0!$. 一次遍历就得到了答案. 由于每一次要统计前面有多少小于它的数字已经被占用了, 所以时间复杂度为$O(n^2)$. 如果使用树状数组维护这个量, 时间复杂度可以降为$O(nlogn)$ ## 代码 ```cpp #include <bits/stdc++.h> using namespace std; #define mp(x, y) make_pair(x, y) #define FOR(x, y, z) for (int x = y; x <= z; x++) typedef long long ll; #define MOD 998244353 #define N 1000006 int n; int bit[N]; void insert(int x) { for (int i = x; i <= n; i += i & -i) bit[i]++; } int query(int x) { int ans = 0; for (int i = x; i > 0; i -= i & -i) ans += bit[i]; return ans; } int a[N]; ll fac[N]; ll cantor() { ll ans = 1; FOR(i, 1, n) { if (a[i] != 1) { ans += fac[n - i] * (a[i] - 1 - query(a[i] - 1)); ans %= MOD; } insert(a[i]); } return ans; } int main() { cin >> n; fac[0] = 1; FOR(i, 1, n) fac[i] = fac[i - 1] * i % MOD; FOR(i, 1, n) cin >> a[i]; cout << cantor(); return 0; } ``` # 逆康托展开 可以求排列编号, 那么就能用同样的计数方法求给定编号的排列. 整个过程类似于进制转换: 除以当前位的"权"就可以知道这一位该放**在前面未出现的第几个数字**了. 这个可以用**值域线段树**维护, 它可以维护当前时刻任意值域范围内的数字有几个. ## 代码——例题为[洛谷P3014 [USACO11FEB]Cow Line S](https://www.luogu.com.cn/problem/P3014) ```cpp #include <bits/stdc++.h> using namespace std; #define mp(x, y) make_pair(x, y) #define FOR(x, y, z) for (int x = y; x <= z; x++) typedef long long ll; #define int ll #define N 1000006 int n, k; int bit[N]; void insert(int x) { for (int i = x; i <= n; i += i & -i) bit[i]++; } int query(int x) { int ans = 0; for (int i = x; i > 0; i -= i & -i) ans += bit[i]; return ans; } int a[N]; ll fac[N]; ll cantor() { ll ans = 1; FOR(i, 1, n) { if (a[i] != 1) ans += fac[n - i] * (a[i] - 1 - query(a[i] - 1)); insert(a[i]); } return ans; } struct node { int l, r, v; } segtree[N * 4]; void build(int pos, int l, int r) { segtree[pos].l = l; segtree[pos].r = r; if (l == r) { segtree[pos].v = 1; return; } int mid = (l + r) >> 1; build(pos << 1, l, mid); build(pos << 1 | 1, mid + 1, r); segtree[pos].v = segtree[pos << 1].v + segtree[pos << 1 | 1].v; } void dec(int pos, int k) { int mid = (segtree[pos].l + segtree[pos].r) >> 1; if (segtree[pos].l == segtree[pos].r) { segtree[pos].v--; return; } if (k <= mid) dec(pos << 1, k); else dec(pos << 1 | 1, k); segtree[pos].v = segtree[pos << 1].v + segtree[pos << 1 | 1].v; } int query2(int k) // 非递归求整个[1,n]范围内的第k大数字是几 { int pos = 1, l = 1, r = n; while (k) { if (l == r) return l; int ll = segtree[pos << 1].v; if (ll >= k) { r = segtree[pos << 1].r; pos = pos << 1; } else { k -= ll; l = segtree[pos << 1 | 1].l; pos = pos << 1 | 1; } } return 0; } vector<int> decantor(ll n, ll rk) { vector<int> ans; FOR(i, 1, n) { ans.push_back(query2(rk / fac[n - i] + 1)); dec(1, ans.back()); //从可选序列里去掉ans.back() rk %= fac[n - i]; } return ans; } signed main() { cin >> n >> k; fac[0] = 1; FOR(i, 1, n) fac[i] = fac[i - 1] * i; while (k--) { char op; scanf(" %c", &op); if (op == 'P') { build(1, 1, n); int t; cin >> t; auto arr = decantor(n, t - 1); for (auto v : arr) cout << v << " "; cout << endl; } else { FOR(i, 1, n) { scanf("%d", &a[i]); bit[i] = 0; } cout << cantor() << endl; } } return 0; } ``` 这道题是康托展开+逆康托展开。记得开long long,和使用快读。 # 参考文献 * [STL next_permutation 算法原理和自行实现](https://www.cnblogs.com/luruiyuan/p/5914909.html) * [康托展开](https://oi-wiki.org/math/combinatorics/cantor/) © 允许规范转载 打赏 赞赏作者 赞 如果觉得我的文章对你有用,请随意赞赏