Loading... # 1 三分法 对于单峰函数$f(x)$求极值的一种手段。 首先我们**必须知道**$f$的凹凸性才行。以下假设$f$是凹的($f''(x)>0$)。 我们取两个三分点$lmid$和$rmid$,会存在两种情况: 1. $lmid>rmid$ 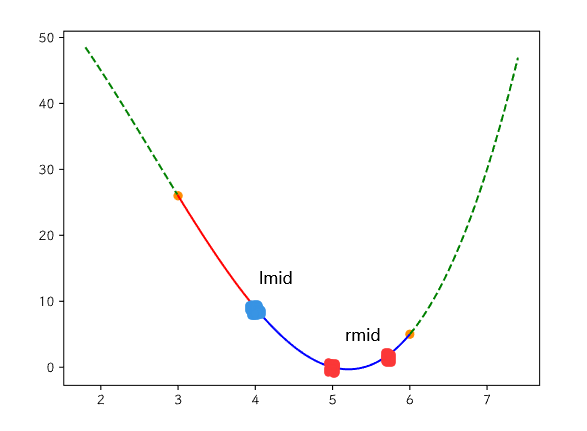 此时容易看出,$rmid$可能位于极值点两侧,所以我们**只能舍弃最左边一段**,也就是令$l:=lmid$ 2. $lmid<rmid$ 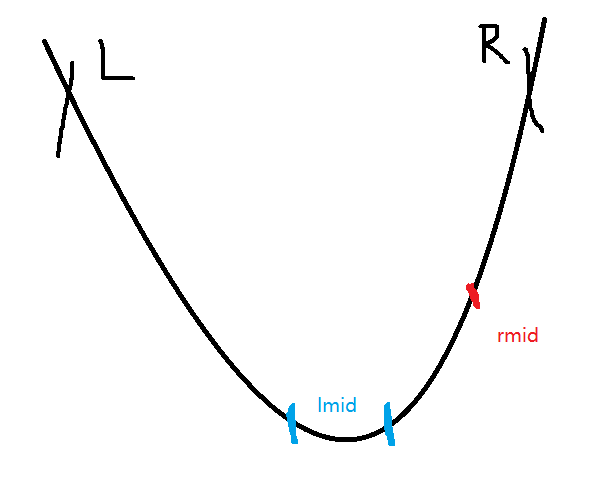 此时同理,$lmid$可能位于极值点两侧,于是我们只能舍弃$rmid$右侧的部分,令$r:=rmid$。 ## lmid和rmid选取 能够看出,为了加快三分速度(把$\log_3$变为近似$\log_2$)复杂度,我们可以令$lmid:=mid-\delta$,$rmid:=mid+\delta$这样去算。注意到$\delta$应该远**小于我们的误差界**。 # 2 实数三分 ## 模板题  ### 代码 ```cpp #include <bits/stdc++.h> using namespace std; #define endl '\n' #define ends ' ' #define FOR(x, y, z) for (auto x = y; x <= z; x++) #define N 1003 int n; double l, r; vector<double> a; double f(double x) { double ans = 0; FOR(i, 0, a.size() - 1) ans += a[i] * pow(x, i); return ans; } double eps = 1e-5; double tri() { double ll, rr; while (abs(l - r) >= eps/10) { double mid = (l + r) / 2; ll = mid - eps / 100, rr = mid + eps / 100; if (f(ll) < f(rr)) l = ll; else r = rr; } return l; } int main() { cin >> n >> l >> r; FOR(i, 1, n + 1) { double x; cin >> x; a.push_back(x); } std::reverse(a.begin(), a.end()); cout << setprecision(6) << tri(); return 0; } ``` ### 细节 绝对误差检测$eps/10$,$lmid$和$rmid$的$\delta$设置为$\epsilon/100$即可。 # 3 整数三分 ## 例题1 20南京F Fireworks ### 题意 做一枚烟花要$n$时间,尝试点燃所有烟花一次要$m$时间,每枚烟花每次被尝试点燃都有$p$的概率成功,求有至少一枚烟花被点燃的**最小**期望时间。 ### 思路 我们称一组操作包含做若干烟花+点燃1次。注意到如果点燃失败,那么实际是无后效性的,所以通过反证容易理解,每组操作中做烟花的数量(我们称之为$k$)都是相同的,那么每组操作的开销就是 $$ nk+m $$ 那么期望代价就是期望操作组数$T$乘上每组开销。 令单次成功概率为$P$,那么众所周知有 $$ T =\frac1P $$ 然后容易知道 $$ P=1-(1-p)^k $$ 从而有 $$ T=\frac1{1-(1-p)^k} $$ 那么期望代价就是 $$ L(k)=\frac{nk+m}{1-(1-p)^k} $$ 由于它是一个关于$k$的函数,我们大胆猜测(或者打表,或者求导)它有一个极小值,那么我们三分即可。 ### 代码 ```cpp #include <bits/stdc++.h> using namespace std; #define endl '\n' #define ends ' ' #define FOR(x, y, z) for (auto x = y; x <= z; x++) typedef long long ll; int t; int n, m; double p; double f(int k) { return (n*(long long)k+m) / (1 - pow(1-p, k)); } double tri() { double ans = DBL_MAX; int l = 1, r = 1000000000; while (r - l > 2) { int mid = (l+r)/2; int lmid = mid, rmid = mid+1; if (f(lmid) > f(rmid)) l = lmid; else r = rmid; } FOR(i,l,r) ans = min(ans, f(i)); return ans; } int main() { cin>>t; while (t--) { cin>>n>>m>>p; p /= 10000; cout<<setprecision(10)<<tri()<<endl; } return 0; } ``` ### 细节 整数二分的时候可以用$ans$解决之前的边界问题,然而整数三分就不能这样解决了。因为有时会遇到$l=lmid$或者$r=rmid$的情形。这时候不如采取一个笨办法:**缩小到足够小区间后枚举**。比如本题就是只做到$r-l\leq2$然后枚举不超过三个值。 ## CF1355E Restorer Distance ### 题意 有$N$堆高度不同的砖,+1、-1、移动1的开销分别为$A$、$R$、$M$,求把它们变得一样高的最小开销。 ### 分析 显然这个开销是关于目标高度$h$的函数,那么我们考虑开销$f(h)$的计算,只要枚举每个位置是需要增加还是减少即可。在全部计算完后,如果$M<A+R$,那么我们可以将$\min(add,del)$的操作转换为移动。 果断猜测这个$f(h)$应该存在最小值,于是做一个整数三分即可。 事实上,通过维护$add$和$del$所需的数量,二分之间的转移是可以通过树状数组加速的。不过没这种必要。 ### 代码 ```cpp #include <bits/stdc++.h> using namespace std; #define endl '\n' #define ends ' ' #define FOR(x, y, z) for (auto x = y; x <= z; x++) typedef long long ll; #define N 100005 int arr[N]; int a, r, m, n; ll f(int h) { ll add = 0, del = 0, mv = 0; FOR(i, 1, n) if (arr[i] < h) add += h - arr[i]; else if (arr[i] > h) del += arr[i] - h; if (m < a + r) { ll d = min(add, del); mv = d, add -= d, del -= d; } return add * a + del * r + mv * m; } ll tri() { int l = 0, r = 1e9; ll ans; while (r - l > 2) { int mid = (l+r)/2; int lm = mid, rm = mid+1; if (f(lm) > f(rm)) l = lm, ans = f(rm); else r = rm, ans = f(lm); } FOR(i,l,r) ans = min(ans, f(i)); return ans; } int main() { cin >> n >> a >> r >> m; FOR(i, 1, n) cin >> arr[i]; cout<<tri(); return 0; } ``` © 允许规范转载 打赏 赞赏作者 赞 如果觉得我的文章对你有用,请随意赞赏