Loading... ## A. Square String? 判断一个字符串前后半部分是否相等. 没啥好说的 ## B. Squares and Cubes ### 题意 给定$n$, 求$[1,n]$有多少平方数或立方数. ### 做法 枚举$[1,\sqrt n]$, 用set计数即可. ## C. Wrong Addition ### 题意 $a+b=s$, 给定$a$和$s$求$b$可能是什么. 惟一的区别是这里的"$+ $"在进位时是在本位和高位之间塞进去一个新的$1$, 而不是进到高位. 如图: 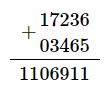 ### 分析 从低位往高位枚举就行了, 如果$a[i]$大, 那么$b[i]=s[j]+10-a[i]$, 同时判断下一位是否为$1$(不是$1$不合法), 然后$j$应该$-=2$跳过进位的$1$; 否则$b[i]=s[j]-a[i]$, $i, j$同时$-=1$即可. 最终判断一下, 如果$s$剩余那么直接放到$b$里, 如果$a$剩余则不合法. ### 代码 ```cpp #include <bits/stdc++.h> using namespace std; #define mp(x, y) make_pair(x, y) #define FOR(x, y, z) for (int x = y; x <= z; x++) typedef long long ll; string a, s; stack<int> b; int t; int solve() { int i = a.size() - 1, j = s.size() - 1; while (i >= 0 && j >= 0) { if (a[i] > s[j]) { if (!j || s[j - 1] != '1') return -1; else { b.push(s[j] + 10 - a[i]); i--; j -= 2; } } else { b.push(s[j] - a[i]); i--; j--; } } if (i >= 0) return -1; while (j >= 0) { b.push(s[j] - '0'); j--; } return 0; } int main() { cin >> t; while (t--) { cin >> a >> s; int ans = solve(); if (ans == -1) { cout << -1 << endl; while (!b.empty()) b.pop(); } else { while (!b.empty() && b.top() == 0) b.pop(); while (!b.empty()) { cout << b.top(); b.pop(); } cout << endl; } } return 0; } ``` ## D. New Year's Problem ### 题意&做法1 见[[算法]二分专题](https://zclll.com/index.php/algo/binary_search.html) ### 做法2 首先处理出每个人可能得到的喜悦的最小值, 答案不能超过这个值. 既然只能选$n-1$个, 那么就要有**一家店满足两个人**, 在这个意义上, 我们应该考察每家店的**第二大**值. 选择其中最大的那个满足两个人, 然后其他$n-2$家店选$n-2$个人的最大值就行了. 因此答案就是 $$ min(max_{\forall people}\{v\}, second\_great_{\forall shops}\{v\}) $$ ### 代码2 ```cpp #include <bits/stdc++.h> using namespace std; #define mp(x, y) make_pair(x, y) #define pb(x) push_back(x) #define FOR(x, y, z) for (int x = y; x <= z; x++) typedef long long ll; typedef pair<int, int> pii; int t, m, n; #define N 100005 int maxx[N]; int second(const vector<int> a) { int mx1 = 0, mx2 = 0; for (auto &v : a) if (v > mx1) mx2 = mx1, mx1 = v; else if (v > mx2) mx2 = v; return mx2; } int main() { cin >> t; while (t--) { cin >> m >> n; // visit at most n-1 shops memset(maxx, 0, sizeof(maxx)); int ans = 0; FOR(i, 1, m) { vector<int> tmp; tmp.clear(); FOR(j, 1, n) { int x; cin >> x; tmp.emplace_back(x); if (x > maxx[j]) maxx[j] = x; } ans = max(ans, second(tmp)); } int minn = *min_element(maxx + 1, maxx + n + 1); //记录每个人可能得到的最大值, 答案不能超过这个值. cout << min(ans, minn) << endl; } return 0; } ``` ## E. MEX and Increments ### 题意 给定一个数组, 长度为$n$, 所有元素$a_i\in[1, n]$. 对于所有的$MEX\in[0,n]$, 请给出需要多少步操作. $MEX$指的是数列中**最小未出现整数** 可以采取的每步操作是把任意数字+1, 对每个数字操作没有次数限制. ### 分析 对于每个$MEX$, 应当递推维护$[0, MEX-1]$所有数字的贡献$ctb$, $ctb_i$显然可以由$ctb_{i-1}$递推得来. 只要在$cnt[MEX-1]==0$的情况下找到$[0, MEX-1]$里面最靠右的$cnt[v]>1$的$v$即可用$v$来填补$MEX-1$使上述区间连续. 这时有 $$ ctb_{i-1}=ctb_i+MEX-1-v $$ 这个贪心的正确性非常显然. 这个$v$的查找可以维护一个$stack$维护到当前为止所有出现超过一次的$v$, 出现几个就入几个, 使用时$pop$即可. 对于每一个答案, 还需要加上$cnt[MEX]$——当前数字出现的次数, 这一部分不需要维护到$ctb$里面去. ### 代码 ```cpp #include <bits/stdc++.h> using namespace std; #define mp(x, y) make_pair(x, y) #define FOR(x, y, z) for (int x = y; x <= z; x++) typedef long long ll; #define N 200005 int t, n; ll cnt[N]; int main() { cin >> t; while (t--) { int n; cin >> n; memset(cnt, 0, sizeof(cnt)); FOR(i, 1, n) { int tt; cin >> tt; cnt[tt]++; } stack<int> ab; while (!ab.empty()) ab.pop(); FOR(i, 2, cnt[0]) ab.push(0); cout << cnt[0] << ' '; ll ans = 0; FOR(mex, 1, n) // mex左侧完整, 自身缺失 { if (!cnt[mex - 1]) { if (ab.empty()) { FOR(i, mex, n) cout << -1 << ' '; break; } else { int tt = ab.top(); ab.pop(); cnt[mex - 1] = 1; ans += mex - 1 - tt; cout << cnt[mex] + ans << ' '; } } else cout << cnt[mex] + ans << ' '; FOR(i, 2, cnt[mex]) ab.push(mex); } cout << endl; } return 0; } ``` ## F. Let's Play the Hat? ### 题意 $n$个人分$m$张桌子玩游戏, 玩$k$轮, 每张桌子每轮必须是$\lceil \frac{n}{m}\rceil$或者$\lfloor \frac{n}{m}\rfloor$人, 任意时刻不能出现两人, 使得其在多人桌游戏的轮数相差超过1. ### 分析 多人桌和少人桌的数量及人数都很好求, 那么直接贪心就可以了. 尽量把上多人桌次数少的人在当前轮安排在多人桌. ### 代码 ```cpp #include <bits/stdc++.h> using namespace std; #define mp(x, y) make_pair(x, y) #define FOR(x, y, z) for (int x = y; x <= z; x++) typedef long long ll; typedef pair<int, int> pii; int t; int n, m, k; void solve() { vector<pii> a; FOR(i, 1, n) { a.push_back(mp(i, 0)); } int bt = n % m, st = m - bt; int big = n / m + (bool)(n % m), small = n / m; FOR(i, 1, k) { FOR(j, 0, bt - 1) { cout << big << " "; FOR(l, 0, big - 1) { cout << a[j * big + l].first << " "; a[j * big + l].second++; } cout << endl; } FOR(j, 0, st - 1) { cout << small << " "; int tt = big * bt; FOR(l, 0, small - 1) { cout << a[j * small + l + tt].first << " "; } cout << endl; } sort(a.begin(), a.end(), [](const pii &a, const pii &b) { return a.second < b.second; }); } cout << endl; } int main() { cin >> t; while (t--) { cin >> n >> m >> k; solve(); } return 0; } ``` ## G. Unusual Minesweeper ### 题意 二维平面上有$n$个炸弹, 每个炸弹爆炸会引爆和自己在一条直线且距离不超过$k$的其他炸弹, 可以连锁反应. 每个炸弹都有自己的倒计时, 同时, 你每秒钟也可以主动引爆一个炸弹. 问所有炸弹引爆完毕最少要多久. ### 分析 首先拆分出所有的连通分量, 每个连通分量的引爆时间是其中爆炸最早的炸弹引爆时间. 那么每秒引爆最晚的一个连通分量就可以了. 分连通分量这一块我是用并查集写的, std给的是DFS, 感觉差不多. 并查集顺便练习一下维护集合可并信息(分量最小时间)了. ### 代码(还没调完) ```cpp #include <bits/stdc++.h> using namespace std; #define mp(x, y) make_pair(x, y) #define pb(x) push_back(x) #define FOR(x, y, z) for (int x = y; x <= z; x++) typedef long long ll; typedef pair<int, int> pii; #define N 200005 int t, n, k; struct node { int x, y, t; node() = default; node(int x, int y, int t) : x(x), y(y), t(t) {} }; vector<node> a; vector<int> times; map<int, vector<int>> rows, columns; bool vis[N]; int fa[N], mint[N]; int find(int x) { if (fa[x] == x) return x; return fa[x] = find(fa[x]); } void merge(int x, int y) { x = find(x); y = find(y); fa[x] = y; mint[y] = min(mint[x], mint[y]); } void init() { FOR(i, 0, n - 1) fa[i] = i; a.clear(); times.clear(); memset(vis, 0, sizeof(vis)); rows.clear(); columns.clear(); } int main() { cin >> t; while (t--) { cin >> n >> k; init(); FOR(i, 0, n - 1) { int x, y, t; cin >> x >> y >> t; a.push_back({x, y, t}); mint[i] = t; if (rows.find(x) != rows.end()) { vector<int>::iterator it = lower_bound(rows[x].begin(), rows[x].end(), y); vector<int>::reverse_iterator it2 = it; it2--; while (it != rows[x].end()) { if (a[*it].y - a[i].y > k) break; merge(i, *it); it++; } while (it2 != rows[x].rend()) { if (a[i].y - a[*it2].y > k) break; merge(i, *it2); it2--; } } rows[x].pb(y); if (columns.find(y) != columns) { vector<int>::iterator it = lower_bound(columns[y].begin(), columns[y].end(), x); vector<int>::reverse_iterator it2 = it; it2--; while (it != columns[y].end()) { if (a[*it].x - a[i].x > k) break; merge(i, *it); it++; } while (it2 != columns[y].rend()) { if (a[i].x - a[*it2].x > k) break; merge(i, *it2); it2--; } } columns[y].pb(x); } FOR(i, 0, n - 1) if (fa[i] == i) times.push_back(mint[i]); sort(times.begin(), times.end()); int now = -1, j = times.size(); // now 和 j 都是已经引爆的炸弹 for (int i = 0; i < times.size(); i++) { int t = times[i] - now; if (j - t <= i) { cout << times[i] + j - i << endl; break; } else j -= t; now = times[i]; } } return 0; } ``` 还没调完, 明天起来再说吧 ## H. Permutation and Queries ### 题意 给定一个长度为$n$的全排列$p$, 要求支持两个操作: 1. 交换$p_x$和$p_y$ 2. 给定$i$和$k$, 求$i = p_i$执行$k$次以后的$i$ ### 分析 打的时候考虑了一个环上倍增的做法, 没完全想出来(明天起来再想想), 赛后看到std给了一个分块, 确实是非常巧妙. 首先这是一个图论题, 里面会有若干环, 会多次询问环上的点的移动结果. 并且会进行拆环重组操作. 考虑操作1, 实际是$p_x$的下标$x$和$p_y$的下标$y$换了, 它们的出边并没有换, 所以这个操作很容易完成, 见下图: 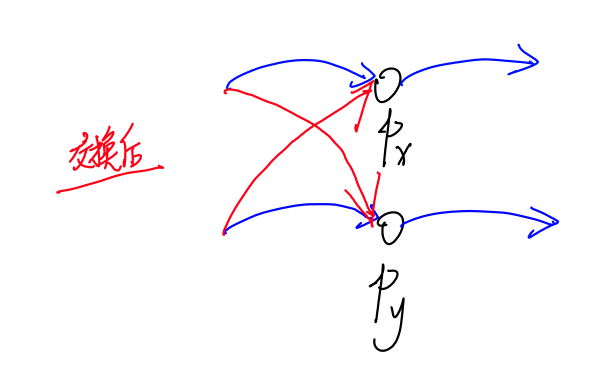 操作2的询问路径可能很长, 显然不能每次都算, 必然要预处理. 然而预处理所有点并不现实, 所以要么预处理**特定长度**, 要么预处理**特定点**到本环其他点的长度. 题解用了一个经典的分块思想, 预处理所有点的$\sqrt n$长度后的点, 那么容易知道任意查找和修改时间复杂度就压到了$O(\sqrt n)$, 可以通过此题. 观察上图, 应当知道要记录$pre$数组, 然后修改时对$pre$进行修改. 因为我们只需要$\sqrt n$长度的信息, 所以单次修改新处理的点也是$O(\sqrt n)$的. ### std ```cpp #include <bits/stdc++.h> //#define int long long #define ld long double #define x first #define y second #define pb push_back using namespace std; const int Q = 100; int n, q, p[100005], r[100005], a[100005]; int32_t main() { ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0); cin >> n >> q; for(int i = 0; i < n; i++) { cin >> p[i]; p[i]--; } for(int i = 0; i < n; i++) r[p[i]] = i; for(int i = 0; i < n; i++) { int x = i; for(int j = 0; j < Q; j++) x = p[x]; a[i] = x; } while(q--) { int t, x, y; cin >> t >> x >> y; if(t == 2) { x--; while(y >= Q) { y -= Q; x = a[x]; } while(y--) x = p[x]; cout << x + 1 << "\n"; } else { x--; y--; swap(r[p[x]], r[p[y]]); swap(p[x], p[y]); int ax = x; for(int i = 0; i < Q; i++) ax = p[ax]; int x2 = x; for(int i = 0; i < Q; i++) { a[x] = ax; x = r[x]; ax = r[ax]; } swap(x, y); ax = x; for(int i = 0; i < Q; i++) ax = p[ax]; x2 = x; for(int i = 0; i < Q; i++) { a[x] = ax; x = r[x]; ax = r[ax]; } } } } ``` © 允许规范转载 打赏 赞赏作者 赞 如果觉得我的文章对你有用,请随意赞赏